УДК 373.3.016:51

О.В. Головня,

студентка 4 курса педагогического факультета

(научный руководитель – С.В. Гадзаова, старший преподаватель)

ОБУЧЕНИЕ РЕШЕНИЮ ЗАДАЧ С ПРОПОРЦИОНАЛЬНЫМИ ВЕЛИЧИНАМИ НА УРОКЕ МАТЕМАТИКИ В 3 КЛАССЕ

В статье обоснована необходимость использования различных методических приемов в процессе формирования умений решать задачи с пропорциональными величинами.

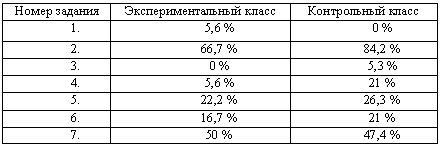
В начальных классах рассматриваются задачи, связанные с пропорциональными величинами: цена-количество-стоимость, скорость-время-расстояние и другие. К основным видам этих задач относятся задачи на нахождение четвертого пропорционального, на пропорциональное деление и на нахождение неизвестных по двум разностям.

Решение задач с пропорциональными величинами вызывает значительные трудности у младших школьников. Одна из причин заключается в том, что понятие «пропорциональная зависимость» не является предметом специального изучения и усвоения [1, с. 226]. Именно поэтому методика работы над такими задачами должна обеспечивать наиболее полную реализацию их обучающего потенциала.

Связи между пропорциональными величинами раскрываются с помощью решения простых задач на нахождение одной из величин по данным, соответствующим значениям двух других величин (например, задача на нахождение стоимости по известным цене и количеству). Поэтому при решении простых задач с пропорциональными величинами (а затем и составных) целесообразно использовать методические приемы, способствующие формированию у учащихся представлений о пропорциональной зависимости величин. К таким приемам  относятся: интерпретация текста задачи с помощью таблицы и чертежа; сравнение результатов решения задач, в которых изменяется одно из данных; составление и решение обратных задач; выбор решения задачи; анализ текстов задач с недостающими и лишними данными [1, с. 227].

Решение задачи разными способами, получение из нее новых, более сложных задач и их решение в сравнении с решением исходной задачи, другие приемы творческой работы создают предпосылки для формирования у ученика умения находить свой «оригинальный» способ решения задачи, воспитывают стремление вести самостоятельно поиск решения новой задачи, той, которая раньше ему «не встречалась». Поиск разных путей решения задач с пропорциональными величинами способствует осознанию причинно-следственных связей, накоплению представлений о функциональной зависимости величин, осуществлению подготовки учеников начальных классов к изучению функций в последующих классах [2, с. 45].

Однако в практике обучения возможности задач с пропорциональными величинами в осуществлении функциональной пропедевтики и развитии математического мышления учащихся, как правило, не используются из-за временных затрат на подготовку и проведение такой работы на уроке. Недостатки методики обучения, на наш взгляд, характеризуются невниманием к интерпретации текста задачи с помощью таблицы и чертежа, игнорированием приемов творческой работы над задачей.

С целью выявления уровня умений решать задачи с пропорциональными величинами было проведено исследование на базе третьих классов СШ № 11 г. Гродно в 2010–2011 учебном году. Были определены экспериментальный класс – 3 «А» (18 человек) и контрольный – 3 «Б» (19 человек). Следует отметить, что математику в обоих классах преподает один учитель.

Для проведения констатирующего этапа эксперимента нами была составлена проверочная работа из 7 заданий, в которых предлагалось выбрать выражение, являющееся решением задачи (1), подставить в граф-схему нужные числа (2), заполнить таблицу к задаче (3), решить задачу на нахождение четвертого пропорционального (4), написать пояснения к действиям (5), выбрать правильный чертеж (6), решить задачу на движение (7). В таблице (таблица 1) представлены результаты правильности выполнения заданий проверочной работы.

Таблица 1 – Результаты правильности выполнения проверочной работы на констатирующем этапе эксперимента

Результаты констатирующего эксперимента позволили сделать вывод о том, что учащиеся 3 «А» и 3 «Б» классов показали практически одинаковый уровень умений решать задачи. Наиболее низкие показатели в заданиях, связанных с интерпретацией текста задачи в виде таблицы и чертежа, при решении задачи на нахождение четвертого пропорционального способом отношения. Вопреки ожиданиям простая задача на движение, являющаяся на данный момент задачей нового вида для учащихся 3 класса, вызвала меньше трудностей. Констатирующий эксперимент показал необходимость целенаправленной работы по обучению решению задач с пропорциональными величинами.

На обучающем этапе эксперимента нами была составлена и апробирована специальная серия заданий, позволяющая реализовать различные приемы работы над задачами с пропорциональными величинами. Рассмотрим некоторые из них:

 – Постройте чертеж и решите задачу: «В 3 ведрах 31 л молока. Сколько молока в 9 таких же ведрах?»

Выбор чертежа позволяет выявить, правильно ли понимает учащийся связь между величинами и характер отношений.

– Решите задачу двумя способами: «В 6 одинаковых домах 24 подъезда. Сколько подъездов в 12 таких же домах?»

– Составьте граф-схему решения задачи: «В 4 тетрадях 48 листов. Сколько листов в 7 таких же тетрадях?»

– Выберите выражение, которое является решением задачи: «Бабушка связала 4 одинаковые шапочки из 12 мотков шерсти. Сколько мотков шерсти понадобиться на 8 таких шапочек?»

а) 12 : 4 ∙ 8 = 24 (м.)

б) 12 : 4 – 8 = 5 (м.)

в) 12 ∙ (8 : 4) = 24 (м.)

г) 12 : (8 – 4 ) = 3 (м.)

Особенностью данного задания является то, что выбор решения задачи следует осуществить среди выражений, представляющих наряду с неверными два верных решения задачи разными способами.

– Постройте таблицу и решите задачу: «На пошив 8 одинаковых пальто израсходовали 24 м ткани. Сколько ткани потребуется на 2 таких же пальто?»

Мы также использовали различные методы и формы работы: самостоятельная работа, проблемный метод, использование опорных схем; работа в парах и группах, работа на карточках.

С целью проверки эффективности проделанной работы был проведен контрольный эксперимент. В таблице 2 представлены результаты правильности выполнения заданий проверочной работы.

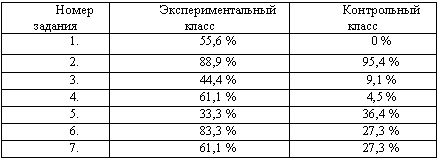
Таблица 2 – Результаты правильности выполнения проверочной работы на контрольном этапе эксперимента

Результаты контрольного этапа эксперимента свидетельствуют о том, что процент учащихся экспериментального класса, справившихся с заданиями, превышает соответствующий процент учащихся контрольного класса.

На основании метода углового преобразования Фишера была оценена достоверность различий между процентными долями экспериментального и контрольного классов. Экспериментальное значение Ф* находится в зоне значимости по четырем показателям (1, 3, 4 и 6 задания), в зоне неопределенности по одному показателю (7-е задание), в зоне незначимости в двух случаях (2, 5 задания).

Исследование показало, что работа над задачами с пропорциональными величинами с использованием вариативных методических приемов, заданий творческого характера эффективно влияет на развитие умений решать задачи с пропорциональными величинами и обеспечивает функциональную пропедевтику.

In the article substantiated the necessity  of using various methodical techniques in the process of formation  abilities of doing a sums with proportional sizes.

Список литературы

1. Истомина, Н.Б. Методика обучения математике в начальных классах: учеб. пособие для студ. сред. и высш. учеб. заведений / Н.Б. Истомина. – 3-е изд. – М.: «Академия», 2000. – 288 с.

2. Гребенникова, Н.Л. Решение задач на зависимость величин разными способами / Н.Л. Гребенникова // Начальная школа. – 1999. – № 2. – С. 45–50.