УДК 373.3.016:51

Д.А. Борисюк,

студентка 4 курса педагогического факультета

(научный руководитель – С.В. Гадзаова, старший преподаватель)

ОСОБЕННОСТИ РАБОТЫ НАД ЗАДАЧАМИ НА ДВИЖЕНИЕ В НАЧАЛЬНЫХ КЛАССАХ

В статье обоснована необходимость использования различных методов и приемов в формировании умений решать задачи на движение.

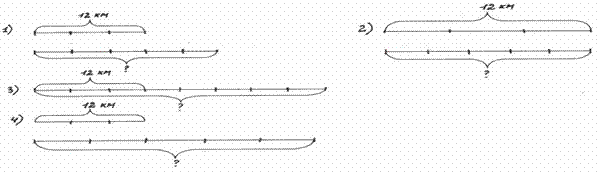
Математическая задача помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. В то же время решение задач способствует развитию младших школьников.

Задачи на движение вводятся в 3 классе. Учащиеся знакомятся с величинами «скорость», «время», «путь» и должны понимать, что подразумевается под такими понятиями, как путь, пройденный в единицу времени, отрезок пути, который прошел объект за определенное время [1, с. 58].

Решение задач на движение, также как и задач с пропорциональными величинами, вызывают значительные трудности у младших школьников. Поэтому при обучении решению задач на движение необходимо использовать различные приемы: интерпретация текста задачи с помощью таблицы и чертежа, сравнение результатов решения задач, в которых изменяется одно из данных, составление и решение обратных задач, выбор решения задачи, анализ текстов задачи с недостающими и лишними данными, приемы творческой работы над задачами [2, с. 227].

Следует отметить, что задача на движение является своего рода задачей с пропорциональными величинами, рассматриваемой в динамике. Поэтому особенностью работы над задачей на движение является интерпретация текста задачи в виде чертежа.

С целью выявления уровня умений решать задачи на движение и задачи с пропорциональными величинами нами было проведено исследование на базе третьих классов СШ № 11 г. Гродно и гимназии № 5 г. Гродно в 2010–2011 учебном году. Были определены экспериментальный класс – 3 «В» (16 человек) и контрольный – 3 «Б» (15 человек).

Для проведения констатирующего этапа эксперимента нами была составлена проверочная работа из 5 заданий для 2 вариантов, в которых предлагалось решить задачу на движение, выбрать выражение, являющееся решением задачи, выбрать правильный чертеж, заполнить таблицу к задаче с пропорциональными величинами и решить ее, заполнить граф-схемы к задаче.

Результаты констатирующего эксперимента позволили сделать вывод о том, что наиболее низкие показатели в заданиях, связанных с интерпретацией текста задачи в виде таблицы, чертежа и граф-схемы. Наиболее высокие показатели в задании, связанном с задачей нового вида для учащихся, – задачей на движение. Констатирующий эксперимент показал, что необходима целенаправленная работа по обучению общим приемам работы над задачами с пропорциональными величинами.

На обучающем этапе эксперимента нами была составлена и апробирована специальная серия заданий, которая позволяет реализовать различные приемы работы над задачами разных типов, но в основном – над задачами на движение. Вот некоторые из них:

– Выберите правильный чертеж к условию задачи.

«Турист за 3 часа прошел 12 км. Какое расстояние он пройдет за 5 ч, если будет идти с той же скоростью».

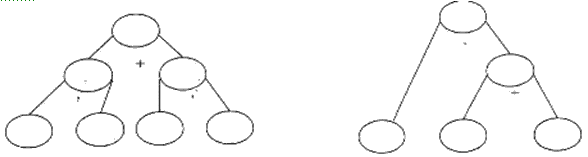
Как показала проверочная работа на констатирующем этапе эксперимента, задание, связанное с интерпретацией текста задачи в виде чертежа, вызвало наибольшие трудности у учащихся. Поэтому на уроках часто использовались задания, направленные на выбор чертежа и установление связей между величинами.

– Выберите выражение, которое является решением задачи, и подчеркните его.

«За 6 часов велосипедист проезжает 120 км. Сколько километров проезжает велосипедист за 2 часа?»

1) 120 : (6 • 2) = 10 (км)

2) 120 : (6 – 2) = 30 (км)

3) 120 : 6 • 2 = 40 (км)

4) 120 : (6 : 2) = 40 (км)

В данном задании необходимо выбрать среди представленных записей 2 верных решения задачи. При выполнении этого задания учащиеся смогли заметить лишь один верный вариант, что свидетельствует о несформированности представлений о пропорциональной зависимости величин.

– Заполните таблицу к задаче. Запишите решение и ответ.

«За 5 часов велосипедист проезжает 60 км, а автомобиль 325 км. На сколько скорость автомобиля больше скорости велосипедиста?»

Задания такого вида также систематически использовались нами, так как построение и заполнение таблиц вызывает трудности у учащихся.

– Прочитайте задачу и подставьте в граф-схемы нужные числа.

«В магазин с утра привезли 5 ящиков моркови по 10 кг в каждом. После обеда привезли еще 4 таких же ящика с картофелем. Сколько килограммов овощей привезли за день?»

Данное задание направлено на установление взаимосвязей между величинами, что вызывает значительные трудности у учащихся. Как показала проверочная работа на констатирующем этапе эксперимента, учащиеся смогли заполнить только одну граф-схему.

На уроках применялись такие виды и формы работ, как работа в группах, парах, самостоятельная работа; математические диктанты, тестирование. Для закрепления умения решать задачи также использовались упражнения творческого характера: составление задач учащимися, преобразование данных задач, сравнение задач, сравнение решений задач.

Таким образом, исследование показывает, что работа над задачами на движение должна основываться на установлении взаимосвязей между компонентами задачи, использовании различных приемов и методов работы над задачей, что обеспечивает понимание учащимися решения данного вида задач, а также автоматизм их решения.

In the article substantiated the necessity of using different methods and techniques in formation skills of doing a sums of motion.

Список литературы

1.       Халидов, М.М. Теория и практика обучения младших школьников решению математических задач / М.М. Халидов, В.М. Мукина // Начальная школа. – 2006. - № 9. – С. 57 – 59.

2.       Истомина, Н.Б. Методика обучения математике в начальных классах: учеб. пособие для студ. сред. и высш. учеб. заведений / Н.Б. Истомина. – 3-е изд. – М.: «Академия», 2000. – 288 с.